Since all that GDPR stuff came out a few months back I've been requesting my data from all sorts of sources, simply to see what it is they collect. Some companies are okay, yet others (google) to collect pretty much every metric of information they possibly can.

Discord recently release their "Request all your data" button, intrigued as with other sites I requested it, a few days later a zip file dropped into my inbox.
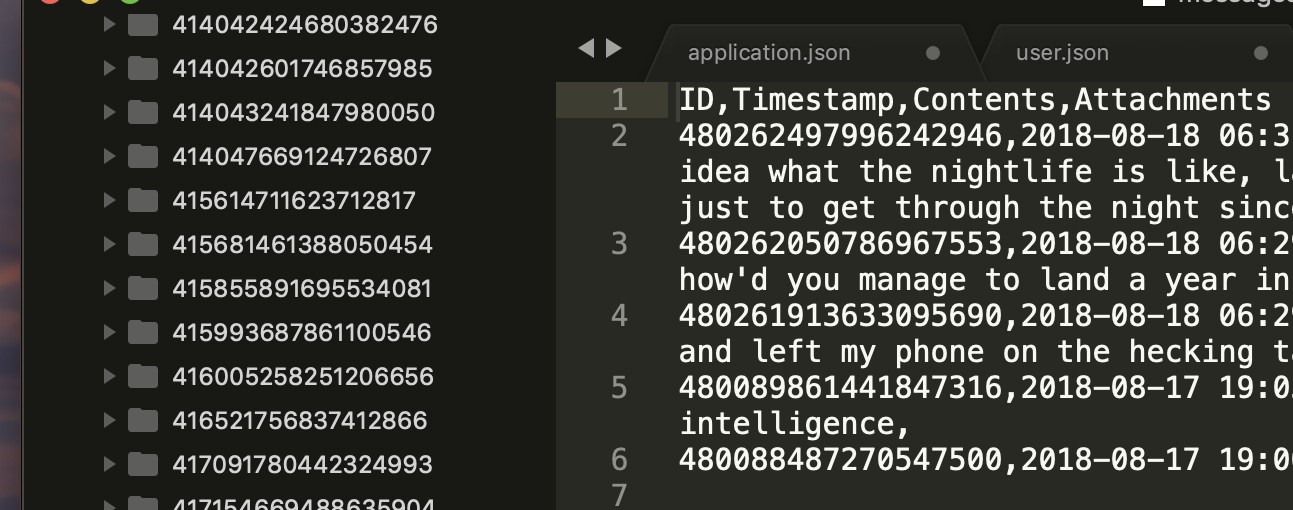
As with other services the data isn't structured very logically, nor are you given much help in understanding just what it is you're looking at, but CSVs are easy enough to understand. Discord obviously keeps every message you've ever posted on every guild (joined or not) and DMs for their indexing and history.
In my case this resulted in 268,814 messages over a period of about 3 years, about 250 messages a day. A lot of data. Scary to think that with enough sophistication someone could accurately piece together your entire personality - alongside all the other metadata that's spread across different services someone with complete access could effectively track and monitor your entire life, they most likely do.
Someone suggested to me that I use all my messages to make a silly chatbot, Markov chains are often used for this (and other things like state machines/game AI) with surprising intelligence at times.
Firstly I needed to extract all the data from the discord dump into something more manageable, removing all the garbage data like timestamps, attachments etc. I wrote this small python script that would collate the information into one big json file.
import os
import csv
import json
c = 0
data = []
for subdir, dirs, files in os.walk("./"):
for file in files:
if file == "messages.csv":
with open(os.path.join(subdir, file)) as f:
# ID,Timestamp,Contents,Attachments
r = csv.reader(f, delimiter=",", quotechar='"')
for row in r:
data.append(row[2])
c += 1
print("\n")
print(str(c) + ' instances')
print("creating json...")
with open('data.json', 'w') as f:
json.dump(data, f)
print("created.")The resulting json file was 7.7mb(!) in size.
Markov chains are quite simple, at least in this case, essentially all that needs to be done is collect each word from each sentence, remove duplicates and order them into a list.
After this we run over every word again, and find the probability that a word succeeds this word and place those words in a dict with a key:value pair of word:number_of_times_occurred.
For example, take these short sentences.
The cat sits.
Sits cat the.
cat cat sits.
Would be ordered firstly into a list of all words,
the: []
cat: []
sits: []
And then gather the occurrences of words after these words,
the: [cat, .]
cat: [sits, the, cat, sits]
sits: [., cat, .]
Reduce the array into a count of each word,
the: {cat: 1, .:1}
cat: {sits: 2, the:1, cat:1}
sits: {.:2, cat:1}

So the probability of the word 'sit' being chosen after the word 'cat' is 2/4,
.5. word_probaility/total_word_count. I should note that this process would
continue indefinitely if not for some ending character, a period is used in this
case, but in the example below I simply appended END_TOKEN to each sentence as
an ending indicator.

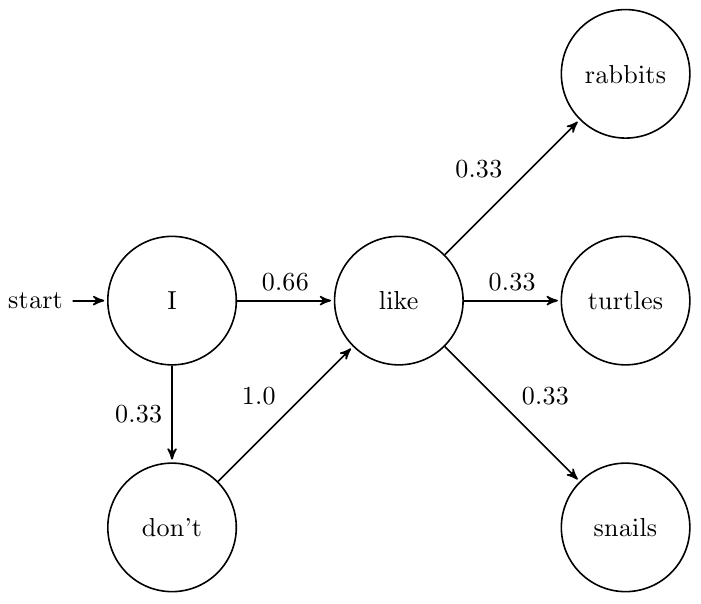
From a real world example, you can see the words 'mad' and 'man' grouped together, so I would've said for example "what a mad man". Here's an image that explains the process a little easier.
Here's the resulting script I wrote for my MoonScript discord bot, Shortbread.
json = require("rxi-json-lua")
inspect = require("inspect")
dataset = {}
dict = {}
isTrained = false
return (...) ->
if select(2, ...)[1] == nil
--no specified usage flag
select(1,...).channel\send("train/post")
return
switch select(2, ...)[1]
--sort the data and train
when "train"
select(1,...).channel\send("Training!")
select(1,...).channel\send("Parsing data.json")
f = assert(io.open("data.json", "rb"))
content = f\read("*all")
f\close()
content = json.decode(content)
select(1,...).channel\send("Attempting to train...")
-- make an empty dict
-- for word in collection
-- if word not in dict
-- add word to dict as key
-- value is a dict
-- that has the following word
-- and set value to 1
-- if word in dict
-- if following word in that word's dict
-- value ++
-- else
-- add word to that words dict
-- value = 1
for _, line in ipairs(content) do
s = {"START_TOKEN"}
for word in line\gmatch("[^ ]+") do
s[#s+1] = word
for key, word in ipairs(s) do
nextWord = ""
z = s[key+1]
if z == nil then
nextWord = "END_TOKEN"
else
nextWord = tostring(s[key+1])
if not dataset[word] then
dataset[word] = {}
if nextWord != nil then
dataset[word][nextWord] = 1
else -- word in dict
if nextWord != nil then
if dataset[word][nextWord] then
dataset[word][nextWord] += 1
else
dataset[word][nextWord] = 1
isTrained = true
select(1,...).channel\send("Training complete.")
return
when "post"
if isTrained
-- To find the probability of the following word
-- take each word's occurrence
-- and divide by total nums in the dict
-- the use that probability to semi-randomly choose the next word based on the last
-- continue until the token that's chosen is a period
myStr = {}
currentWord = "START_TOKEN"
mod = 15
while currentWord != "END_TOKEN"
map = {}
for k, v in pairs(dataset[currentWord]) do
-- fill map with values 'value' times
for i=1, tonumber(v) do
table.insert(map, k)
-- randomly pick one, more values in map == greater prob
-- of selecting it
table.insert(myStr, map[math.random(#map)])
-- let it talk a bit more than just 5 words
if mod > 0
if myStr[#myStr] == "END_TOKEN"
mod -= 1
table.remove(myStr, #myStr)
currentWord = tostring(myStr[#myStr])
s = ""
table.remove(myStr, #myStr)
for _, v in pairs(myStr) do
s = s .. " ".. v
select(1,...).channel\send(s)
else
select(1,...).channel\send("Cass not trained!")
The result:
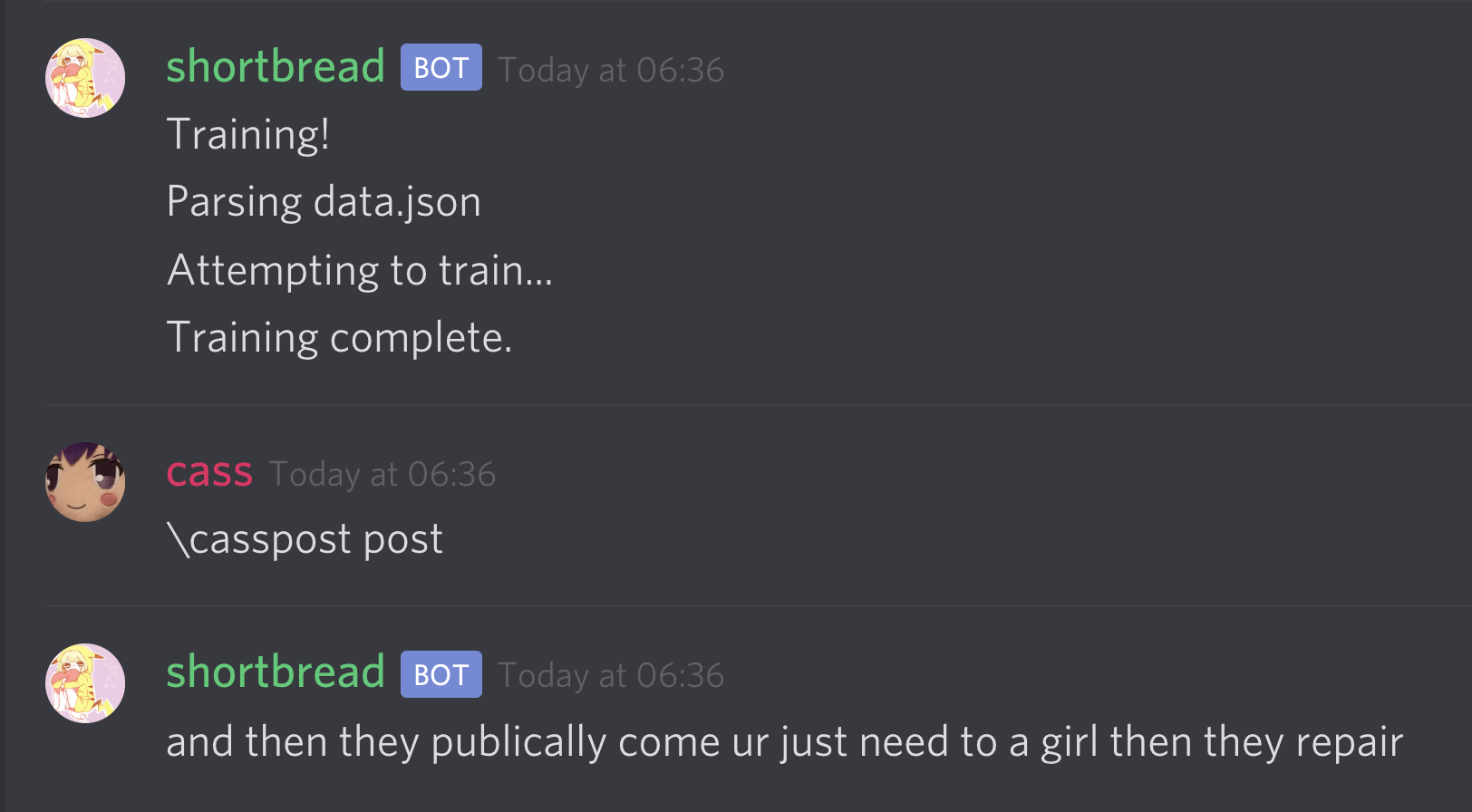
Often times it just spews out complete gibberish because of the low depth of the markov chain, sometimes it is quite eerie when it says something coherent as it imitates my style of speech and typing.
The bot only considers the immediate word in-front, so the 'gibberishness' of sentences can be be reduced by considering not only the word in-front, but the word in-front of that word, and so forth.
